Renewable energy sources, including subterranean heat, oceanic energies, hydroelectric power, and breeze energy, are eco-friendly energy options that have gained increasing consideration from energy inventors and investigators due to their natural influence [1]. These sources of energy are considered eco-friendly because they typically have lower carbon emissions compared to fossil fuels, thereby contributing to mitigating climate change and reducing pollution [2]. Overall, their impact is seen as positive in terms of promoting a cleaner and more sustainable energy future.
Renewable energy technologies typically have a lower environmental impact throughout their life cycles, from extraction and manufacturing to operation and decommissioning and mong these renewable sources, wind energy is currently experiencing rapid expansion [3]. This growth could be driven by various factors such as advancements in technology, supportive government policies, declining costs, and increasing awareness of the environmental benefits of wind power [4]. Currently, researchers are directing their efforts towards enhancing the efficiency of wind power generation in order to accommodate the rising demand for electricity [5].
Wind energy is renewable and can be harnessed in coastal and island regions, where the wind regime is influenced by factors like land-sea wind, topography, and atmospheric pressure [6]. Wind power potential analysis is a central step in identifying suitable locations and technologies for wind energy development [5]. However, this analysis requires reliable and high-resolution data, as well as appropriate numerical methods to perfect the wind distribution and evaluate the wind power density and energy production [7]. Also, climate change has been leading a global temperature rise, which is anticipated to impact wind patterns, resulting in fluctuations in wind speed and direction in numerous regions worldwide [8]. As a result, a multitude of feasibility studies are essential to gather credible data for assessing the sustainability of breeze energy potential at specific study sites [9].
Various numerical methods have been used in previous studies to analyse wind power potential in different settings, based on the availability and quality of wind speed data [10]. These methods include empirical, graphical, analytical, and numerical approaches, each with its own advantages and disadvantages [11]. Some of the most commonly used numerical methods are the standard deviation method, the energy pattern factor method, the wind variability method, maximum likelihood, and the moment method. These methods are based on fitting the Weibull distribution, which is widely accepted as the best representation of the wind speed frequency distribution, to the observed wind speed data [6].
However, different methods may have different levels of accuracy and suitability depending on the characteristics of the study site, such as the wind speed range, the wind speed variability, the data resolution, and the data quality [12]. Therefore, it is important to validate and compare multiple methods to select the best one for a given location. This can be done by using statistical tests, such as the coefficient of determination R2, the root means square error RMSE, and the chi-square test χ2, to measure the goodness of fit between the observed and the modelled wind speed distributions. A higher R2, a lower RMSE, and a lower χ2 indicate a better fit and a more reliable method [13].
Previous studies have assessed wind power potential in similar settings using different numerical approaches, but they have some limitations such as lack of geographic scope, data resolution, and model validation. For example, Akdag and Dinler evaluated multiple sites across Turkey using the power density technique to estimate Weibull parameters via methods such as moments and maximum likelihood [10]. Al-Ghriybah applied the wind variability method in Ajloun, Jordan, and reported a peak speed of 4 m/s but limited potential by global standards [14]. Werapun et al. compared five numerical methods including energy pattern factors, maximum likelihood, modified maximum likelihood, and graphical methods on Phangan Island, Thailand, and found the empirical approach provided the best Weibull fit based on R2 and error percentage [15]. V. Katinas conducted an assessment of breeze energy efficiency in the context of installed turbines, employing the capacity factors as a key metric for the wind speed assessment in more than 18 sites of Lithuania [11]. Also in another investigation, Ko et al. concentrated on connection of meteorological monitoring devices to enhance exactness in surveys on Weno Island, Chuuk State [16]. They applied both Rayleigh and Weibull distribution functions to fit wind speed data [17].
Moreover, there is a gap in the literature regarding the wind power potential of Zanzibar Island, Tanzania, which is a coastal archipelago in East Africa with significant renewable energy opportunities. Zanzibar is currently dependent on the power generated from hydroelectric power plants installed in the Tanzania mainland, which is transmitted through a submarine cable across the Indian Ocean. However, this power supply is unreliable and insufficient, as it is prone to power outages, especially during dry seasons and technical faults. Therefore, there is a need to explore alternative and sustainable sources of energy, such as wind, solar, and tidal energy, to meet the growing demand and to reduce the dependence on fossil fuels.
This study aims to address this gap by assessing four prominent numerical methods (standard deviation, energy pattern factor, wind variability, and moment methods) against high-resolution wind speed data collected over two years at Zanzibar Island. The wind speed and direction data were collected from a meteorological station located at the coastline of Zanzibar, within interval of 30 minutes and a measurement height of 10 meters. The data were processed and analysed, and also the results were compared and validated using statistical tests such as R2, RMSE, and χ2 [18]. The study also identified the most suitable wind turbine models for the site, based on the wind power density, the capacity factor, and the energy production [19]. The study provided valuable insights into the potential of wind energy for Zanzibar’s energy needs, as well as the challenges and opportunities for its development. The study also contributed to the academic discourse on wind energy analysis by presenting a comprehensive and rigorous approach that combines multiple analytical methods with high-resolution local data [20].
Wind information was gathered from the meteorological mast positioned at the Zanzibar site, located at coordinates (60°13’S, 39°13’E). The dataset comprises measurements of wind speed and wind direction, specifically recorded at the actual hub height of 10 meters, covering a period of 24 months from January 2021 to December 2022. These measurements were logged at 30-minute intervals using a Stylists-101 data logger. The site is encompassed by the Indian Ocean, and undergoes four distinct climatic seasons: Spring (March to May), Summer (June to August), Fall/Autumn (September to November), and Winter (December to January). The average temperature fluctuates between 24 and 31 °C, and the annual rainfall is documented at 1,600 mm.
The Weibull distribution has been widely accepted as the most accurate model for representing wind speed distributions due to its flexibility [21]. It assumes wind speeds are independent and identically distributed over time [22]. The double factors Weibull distribution is the most inherent clarity and precision for the wind resources assessment [23]. The model comprises two integral components, namely the Likelihood Density Function (pdf) and the Increasing Distribution Function (cdf). The Weibull likelihood functions to depict wind speed at any time is explicitly defined in eq. (1) [24]:
(1)
Whereby, k and c are the Weibull shape and scale factors respectively, v is the recorded wind speed in m/s. The Weibull scale and shape factors can be obtained using different numerical Weibull fitting methods. The cumulative distribution function results from integrating the Weibull probability density function and represents the cumulative relative frequency within each speed interval. The corresponding cumulative probability function for the Weibull distribution can be expressed as follows eq. (2):
(2)
The wind’s behaviour is described by the shape parameter k, with a small value indicating generally weak wind speeds and a high value suggesting an even distribution of high and low wind speeds at a site. The maximum wind speed vm and most probable wind speed vp are given by eq. (3) and eq. (4) respectively:
(3)
(4)
From these two equations, the gamma function Γ was obtained using eq. (5):
(5)
The study compared four different methods to estimate the Weibull parameters, these methods included Standard Deviation Method (SDM), Energy Pattern Factor Method (EPFM), Moment Method (MOM), and the Wind Variability Method (WVM). Further statistical analysis examined one method with the best fit for the wind resources assessment of the study site.
• Standard deviation method
This technique was primarily recommended by Justus et al. [25], [26]. The standard deviation represents variability from the mean but can be affected more by outliers than other metrics. When both the mean speed and the standard deviation are accessible, the parameter estimation is accomplished through the utilization of the subsequent equations eq. (6) and eq. (7) [24]:
(6)
(7)
The standard deviation σ of the wind speed appeared in eq. (6) was found using eq. (8):
(8)
The average wind speed at any time interval was found using eq. (9):
(9)
• Energy pattern factor
The EPFM calculates the Energy Pattern Factor (EPF) as the cube of the mean cubed wind speed over the cubed mean speed. This method considers the wind speed distribution’s energy profile. High EPF values are generally favorable for wind energy projects because they suggest a stable and reliable source of energy. The energy pattern factor (EPF) can be expressed as per as eq. (10) [27]:
(10)
The values of v ̅^3 and can be found from collected wind speed data. Following the computation of EPF, the Weibull factors were determined utilizing the subsequent mathematical expressions. The scale factor of the distribution is given using eq. (11) while eq. (12) was used to determine respective shape factor of the Weibull distribution:
(11)
(12)
• Moment Method
The MOM estimates k and c directly from the first four moments of the distribution fitted to the data. Through the moment method, the value of k and c were found using eq. (13) and eq. (14) respectively [27], [28]:
(13)
(14)
• Wind Variability Method (WVM)
WVM estimates k based on the variation coefficient which normalizes standard deviation by the mean. This method depicts variability independent of the scale of wind speeds. This empirical method involves determining the value of k based on the wind variability and the average wind speed. The parameters of distribution are given as eq. (15) and eq. (16) [24]:
(15)
(16)
The evaluation of the numerical methods’ performance was conducted through the utilization of three core methodologies, namely Root Mean Square Error (RMSE), Chi-square, and Constant of Determination [27], [29]. The fitted Weibull distributions were compared using the coefficient of determination (R2), Root Mean Square Error (RMSE), and Chi-square test. The value of R2 represents the percent of variation explained by the model, with values closer to 1 indicating a better fit, R2 was determined using eq. (17) whereby, xi , yi and zi are the Weibull occurrence, actual occurrence and the mean wind speed respectively:
(17)
The value of RMSE measures the sample standard deviation of differences between observed and fitted values, with lower values showing less error. Whereby, N is number of the recoded wind speed, n is a time step, xi and yi are the Weibull and actual occurrences. RMSE was calculated using eq. (18):
(18)
The χ2 test examines differences between observed and expected frequencies, with a lower value (closer to the degrees of freedom) demonstrating a better fit distribution [24]. If xi and yi are the actual and frequencies, the Chi-square value can be gives as per as eq. (19) [30]:
(19)
An extrapolation of the Weibull parameter was done in this study using eq. (20) for the shape factor and eq. (21) for the scale factor [26]. The reason for the extrapolation process is due to the fact that, the wind data was collected at the height of 10 meters, and to determine these factors at different height is very important for the wind turbine performance analysis as all analysed wind turbine models in this study have the height greater than 10 meters:
(20)
The extrapolation of the scale factor is given as:
(21)
The value of n can be found using eq. (22) and is stated as follows [31]. Also c0, k0 and h0 are the reference Weibull parameters and height:
(22)
(22)
The potential wind analysis was done by determination of the wind power and wind energy density of the site. Also, the capacity factor analysis was done to give insite on the stability and reliability of the wind resource of the site.
• Wind power and energy estimation
In wind resource assessment, wind power density of the site in W/m^2 can be expressed as in eq. (23) [32]:
(23)
Also, the wind energy density in kWh/m2 density at any projected time T is given as per as eq. (24) below:
(24)
Whereby, c and k are the Weibull constant factors evaluated from numerical method with the best fit, ρ is the air density which is approximately to 1.225 kg/m3, T is the actual time, E/A and P/A are the wind energy and power density W/m2 and kWh/m2 respectively. NREL general power classification was used to classify wind resources of the study site of this research.
The selection of the wind turbine for the wind energy conversion was done in this study by considering two fundamental factors, these factors included the average power output of each proposed turbine model and the capacity or the performance of offered by the respective turbine model. The calculated wind turbine power output was determined using eq. (25) below [18]:
(25)
Whereby, vc, vf and vr are the activation speed, optimal wind speed and rated or halt wind speed of the Wind turbine, also P(e,ave) and PwR are the respective average output and rated power of the proposed turbine models. After determination of the average power from the best fit Weibull parameters in each period of time, the capacity factor can be found using eq. (26):
(26)
All parameters in eq. (25) must be given as a specification, the specifications of the seven turbines are presented in the wind turbine performance analysis results of this research. The proposed turbines started from 50 kW turbine (POLARIS P15-50) to 1 MW wind turbine (BONUS B-1000-54).
The research yielded comprehensive insights into wind energy, analysing wind speed profiles, Weibull parameters, and distributions. Variations in wind speed were examined alongside power and energy densities. The study included a detailed analysis for optimal wind turbine selection based on the observed wind conditions. These findings offer valuable guidance for strategically implementing and optimizing wind energy projects.
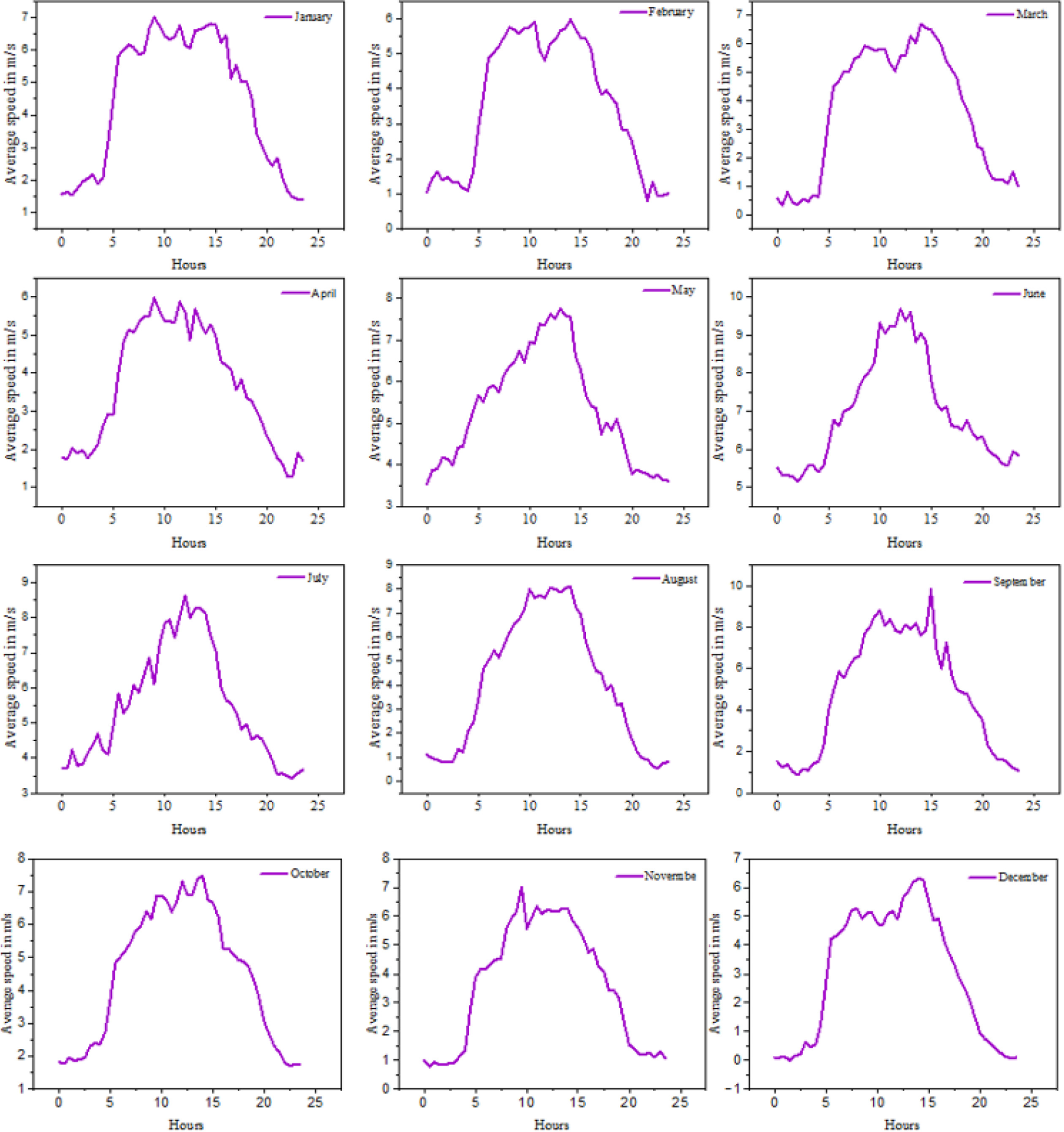
The mean daily wind speed pertains to the average velocity of the wind throughout a 24-hour duration at a particular site. In order to establish the average daily pattern from a given set of raw data, this study computed the mean value of all recorded wind speeds within each half-hour time slot throughout the 24-hour day. For instance, the average wind speed from 12:00 AM to 12:30 AM was calculated, followed by the average for 1:30 AM to 2:00 AM, and so forth for every hour of the day. Most of months have high wind speed within the hour of 5:00 AM to 20:00 PM in 2021 and their wind speed ranges between 3 to 7 m/s. The month of April, June and July have the most variable wind fluctuations as shown in Figure 1. Roughly, the site experienced strong wing 15 hours a day or 5,400 hours (225 days) in 2021.
Daily wind speed profiles for all months of 2021
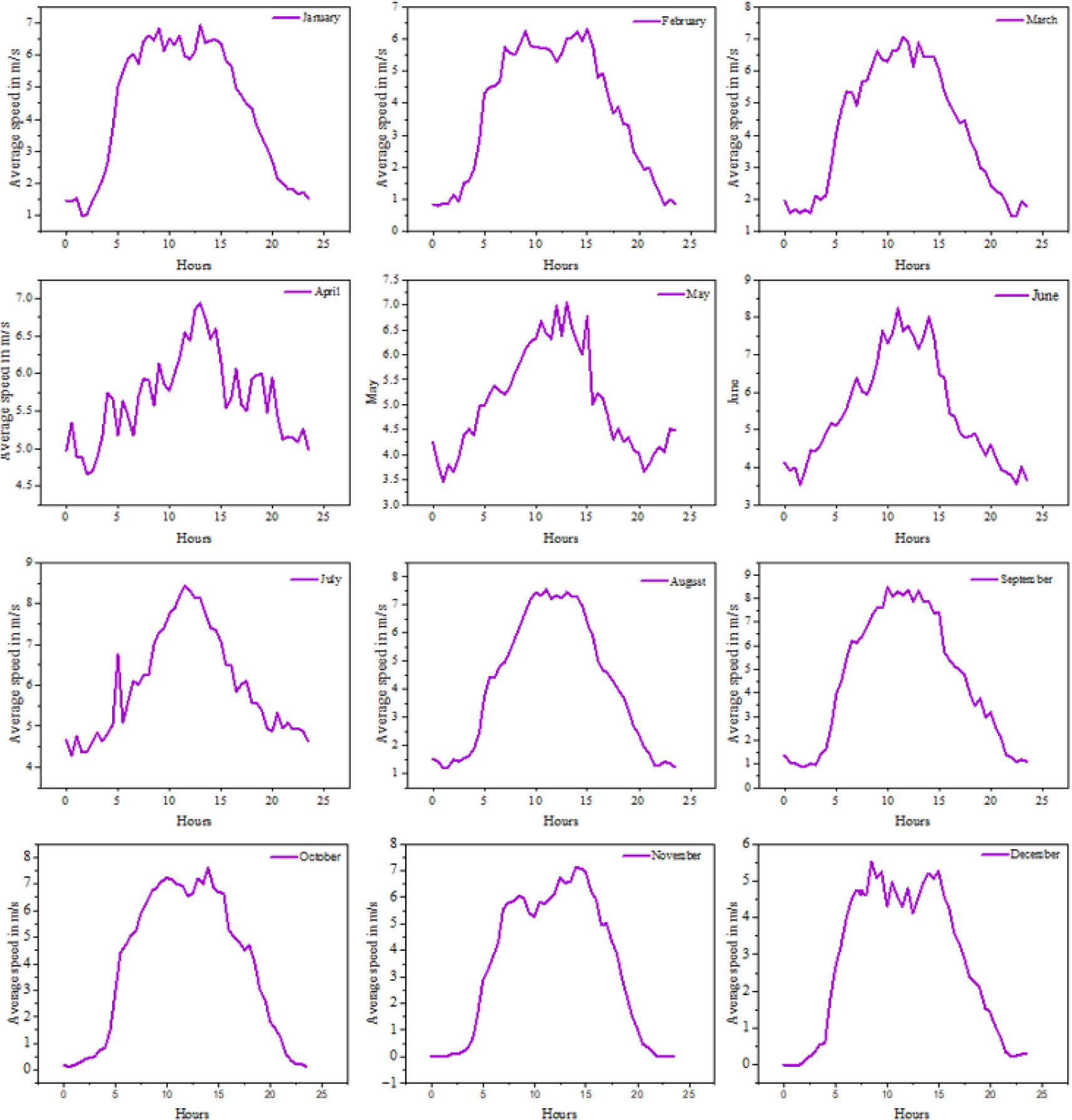
In 2022, the most of the month have high wind speed blows between 5.00 to 20.00 as in 2021, but the month of May, June and July seems to have more variable wind speed. The average most of hours have the wind speed between 3 to 8 m/ as seen in Figure 2. The results show that, the site experienced the strong wind almost 16 hours a day which is equivalent to 5760 hours (240 days) in 2022.
Daily wind speed profiles for all months of 2022
• Hourly standard deviation
The Table 1 and Table 2 below show the hourly standard deviation experienced the site during 2021 and 2022 respectively, in most of the months, more than 22 hours a day shows that wind speed standard deviation tends to be smaller than the average wind speed. The results show that for both 2021 and 2022 have smaller hourly standard deviation in comparison to their respective average wind speed presented in the daily wind speed profiles. More than 90% of daily average wind speed in every hour seems to have speed ranging between 3 to 8 m/s experienced the standard deviation speed ranging between 0 to 2.6 m/s. This indicates that there is less fluctuation in wind speeds over time. Wind speeds are more consistent and predictable, with fewer extreme variations. In the context of wind power generation, low variability means that wind turbines can operate more consistently, leading to higher efficiency and reliability in electricity generation. Wind farms in areas with lower variability may experience more stable outputs over time. Also, Industries and activities sensitive to wind conditions may face fewer challenges related to variability when wind speeds cluster closely around the mean. This can lead to reduced risks in planning and executing operations that depend on consistent wind conditions.
Hourly standard deviation (m/s) for 2021
| Hours | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sept. | Oct. | Nov | 0.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 2.0 | 1.6 | 2.3 | 1.7 | 1.6 | 2.7 | 2.5 | 2.0 | 1.9 | 0.9 | 0.6 | 0.5 |
| 1.00 | 2.1 | 1.8 | 2.3 | 1.4 | 2.1 | 3.0 | 3.0 | 1.9 | 1.8 | 1.2 | 0.7 | 1.1 |
| 2.00 | 1.9 | 1.9 | 2.6 | 1.7 | 2.1 | 2.3 | 2.7 | 2.4 | 1.7 | 1.5 | 1.5 | 1.2 |
| 3.00 | 2.3 | 2.2 | 2.4 | 1.5 | 2.1 | 2.4 | 2.1 | 2.1 | 1.9 | 2.0 | 2.2 | 2.5 |
| 4.00 | 2.4 | 2.3 | 2.6 | 1.3 | 1.5 | 1.8 | 1.8 | 2.3 | 2.1 | 2.4 | 2.1 | 1.9 |
| 5.00 | 1.8 | 2.5 | 2.0 | 1.0 | 1.6 | 1.2 | 9.6 | 2.0 | 2.2 | 1.4 | 1.6 | 1.3 |
| 6.00 | 1.9 | 2.2 | 1.2 | 1.6 | 1.0 | 1.4 | 1.5 | 1.8 | 1.4 | 1.9 | 1.2 | 1.9 |
| 7.00 | 1.5 | 4.2 | 1.6 | 1.0 | 1.3 | 2.9 | 1.3 | 1.2 | 1.7 | 1.7 | 1.3 | 1.5 |
| 8.00 | 1.7 | 1.5 | 1.5 | 1.4 | 1.8 | 1.9 | 1.7 | 1.2 | 1.9 | 2.0 | 1.9 | 1.9 |
| 9.00 | 1.7 | 1.6 | 1.5 | 2.0 | 1.7 | 1.4 | 1.9 | 1.3 | 1.7 | 1.9 | 2.2 | 2.3 |
| 10.00 | 1.9 | 1.9 | 1.9 | 2.0 | 2.2 | 1.9 | 1.6 | 1.6 | 1.8 | 2.3 | 2.3 | 1.9 |
| 11.00 | 2.0 | 1.8 | 1.6 | 1.9 | 2.0 | 3.2 | 1.6 | 1.7 | 2.5 | 2.4 | 1.7 | 1.5 |
| 12.00 | 2.0 | 1.4 | 1.7 | 2.0 | 2.2 | 2.1 | 1.4 | 1.7 | 2.4 | 2.2 | 2.0 | 1.7 |
| 13.00 | 1.8 | 2.0 | 1.9 | 1.9 | 1.9 | 2.0 | 1.8 | 1.5 | 2.2 | 2.0 | 1.6 | 1.4 |
| 14.00 | 1.7 | 1.7 | 1.7 | 1.7 | 2.1 | 2.8 | 2.1 | 1.2 | 1.9 | 1.4 | 1.4 | 2.1 |
| 15.00 | 1.8 | 1.4 | 1.7 | 1.6 | 8.6 | 1.7 | 1.7 | 1.2 | 1.6 | 1.2 | 1.3 | 1.9 |
| 16.00 | 1.2 | 1.2 | 1.8 | 2.0 | 1.8 | 1.6 | 1.4 | 1.2 | 1.3 | 1.0 | 1.8 | 2.0 |
| 17.00 | 1.9 | 1.2 | 1.4 | 2.1 | 1.9 | 2.1 | 1.5 | 1.4 | 1.4 | 1.7 | 1.8 | 2.0 |
| 18.00 | 2.0 | 1.8 | 1.3 | 1.9 | 1.7 | 2.0 | 1.5 | 1.2 | 2.1 | 1.8 | 1.7 | 2.0 |
| 19.00 | 2.0 | 2.0 | 1.9 | 2.0 | 1.9 | 2.2 | 1.7 | 1.6 | 2.2 | 2.1 | 0.9 | 1.7 |
| 20.00 | 2.1 | 2.4 | 2.2 | 2.0 | 1.8 | 2.5 | 2.0 | 2.3 | 2.5 | 2.1 | 0.0 | 1.0 |
| 21.00 | 2.1 | 1.8 | 2.2 | 2.3 | 2.0 | 2.3 | 2.7 | 2.0 | 2.2 | 1.3 | 0.0 | 1.2 |
| 22.00 | 2.3 | 1.6 | 1.9 | 1.6 | 1.9 | 2.6 | 2.4 | 1.9 | 2.1 | 0.9 | 0.0 | 0.0 |
| 23.00 | 2.4 | 1.7 | 2.3 | 1.8 | 1.6 | 2.6 | 2.6 | 1.9 | 1.8 | 0.9 | 0.0 | 0.0 |
Hourly standard deviation (m/s) for 2021
| Hours | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sept. | Oct. | Nov | 0.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 2.4 | 2.2 | 1.4 | 2.3 | 2.3 | 2.4 | 3.0 | 2.2 | 2.7 | 2.8 | 1.9 | 0.5 |
| 1.00 | 2.2 | 2.7 | 1.7 | 2.5 | 2.6 | 2.8 | 3.2 | 1.9 | 2.6 | 3.0 | 1.8 | 0.6 |
| 2.00 | 2.5 | 2.4 | 0.9 | 2.7 | 2.6 | 2.8 | 3.0 | 1.7 | 1.8 | 2.6 | 2.0 | 0.9 |
| 3.00 | 2.8 | 1.9 | 1.1 | 2.4 | 1.8 | 2.3 | 2.3 | 2.0 | 2.1 | 2.8 | 1.9 | 1.5 |
| 4.00 | 2.4 | 1.7 | 1.2 | 2.6 | 2.4 | 2.2 | 2.5 | 2.1 | 2.2 | 2.8 | 2.1 | 1.3 |
| 5.00 | 2.1 | 2.3 | 2.5 | 2.5 | 1.7 | 1.8 | 2.1 | 1.9 | 2.9 | 2.4 | 2.1 | 2.4 |
| 6.00 | 2.0 | 1.4 | 1.7 | 1.8 | 1.2 | 1.5 | 1.5 | 1.5 | 1.4 | 1.8 | 1.6 | 2.5 |
| 7.00 | 1.8 | 2.0 | 1.5 | 1.6 | 1.1 | 1.9 | 1.4 | 1.3 | 2.1 | 2.1 | 2.3 | 3.0 |
| 8.00 | 2.1 | 1.5 | 1.5 | 1.2 | 1.7 | 1.9 | 2.3 | 2.2 | 1.6 | 2.2 | 2.5 | 2.4 |
| 9.00 | 2.6 | 1.5 | 1.7 | 1.9 | 1.5 | 2.0 | 2.1 | 1.9 | 2.0 | 2.1 | 2.5 | 2.5 |
| 10.00 | 2.1 | 1.8 | 1.8 | 2.4 | 1.7 | 1.2 | 1.9 | 1.9 | 1.6 | 2.1 | 2.6 | 2.8 |
| 11.00 | 2.3 | 1.8 | 2.4 | 2.2 | 2.0 | 1.8 | 2.0 | 1.8 | 2.2 | 2.4 | 2.0 | 2.2 |
| 12.00 | 2.0 | 1.7 | 1.5 | 1.9 | 1.6 | 1.9 | 1.8 | 2.0 | 2.2 | 2.5 | 2.0 | 2.3 |
| 13.00 | 2.2 | 1.5 | 1.8 | 2.0 | 1.3 | 1.6 | 1.9 | 2.2 | 1.8 | 2.7 | 1.8 | 2.1 |
| 14.00 | 1.7 | 1.4 | 1.4 | 2.4 | 1.5 | 1.4 | 1.7 | 1.8 | 1.4 | 2.1 | 1.9 | 1.8 |
| 15.00 | 1.8 | 1.7 | 1.5 | 2.4 | 1.5 | 1.3 | 1.9 | 1.5 | 13.4 | 1.8 | 1.9 | 2.7 |
| 16.00 | 1.9 | 1.6 | 1.1 | 2.2 | 1.6 | 1.7 | 1.7 | 1.5 | 1.4 | 1.6 | 1.8 | 2.3 |
| 17.00 | 2.5 | 2.1 | 0.9 | 2.0 | 2.0 | 1.9 | 2.1 | 1.7 | 1.9 | 1.4 | 1.9 | 2.1 |
| 18.00 | 2.2 | 1.7 | 1.3 | 2.2 | 1.7 | 1.8 | 2.4 | 2.0 | 2.2 | 1.8 | 2.1 | 2.1 |
| 19.00 | 2.3 | 2.0 | 2.0 | 2.0 | 1.9 | 1.7 | 2.7 | 2.2 | 2.5 | 2.3 | 2.6 | 2.1 |
| 20.00 | 2.2 | 1.8 | 2.3 | 2.0 | 1.9 | 2.1 | 2.5 | 2.0 | 2.8 | 2.8 | 2.2 | 1.6 |
| 21.00 | 3.3 | 1.9 | 1.9 | 2.4 | 2.1 | 2.2 | 3.0 | 1.8 | 2.9 | 3.1 | 2.1 | 1.4 |
| 22.00 | 2.2 | 2.8 | 1.9 | 2.0 | 2.1 | 2.4 | 2.6 | 1.5 | 3.1 | 2.7 | 2.2 | 0.8 |
| 23.00 | 2.2 | 1.8 | 3.0 | 2.7 | 2.1 | 2.6 | 2.8 | 1.6 | 2.4 | 2.6 | 2.5 | 0.5 |
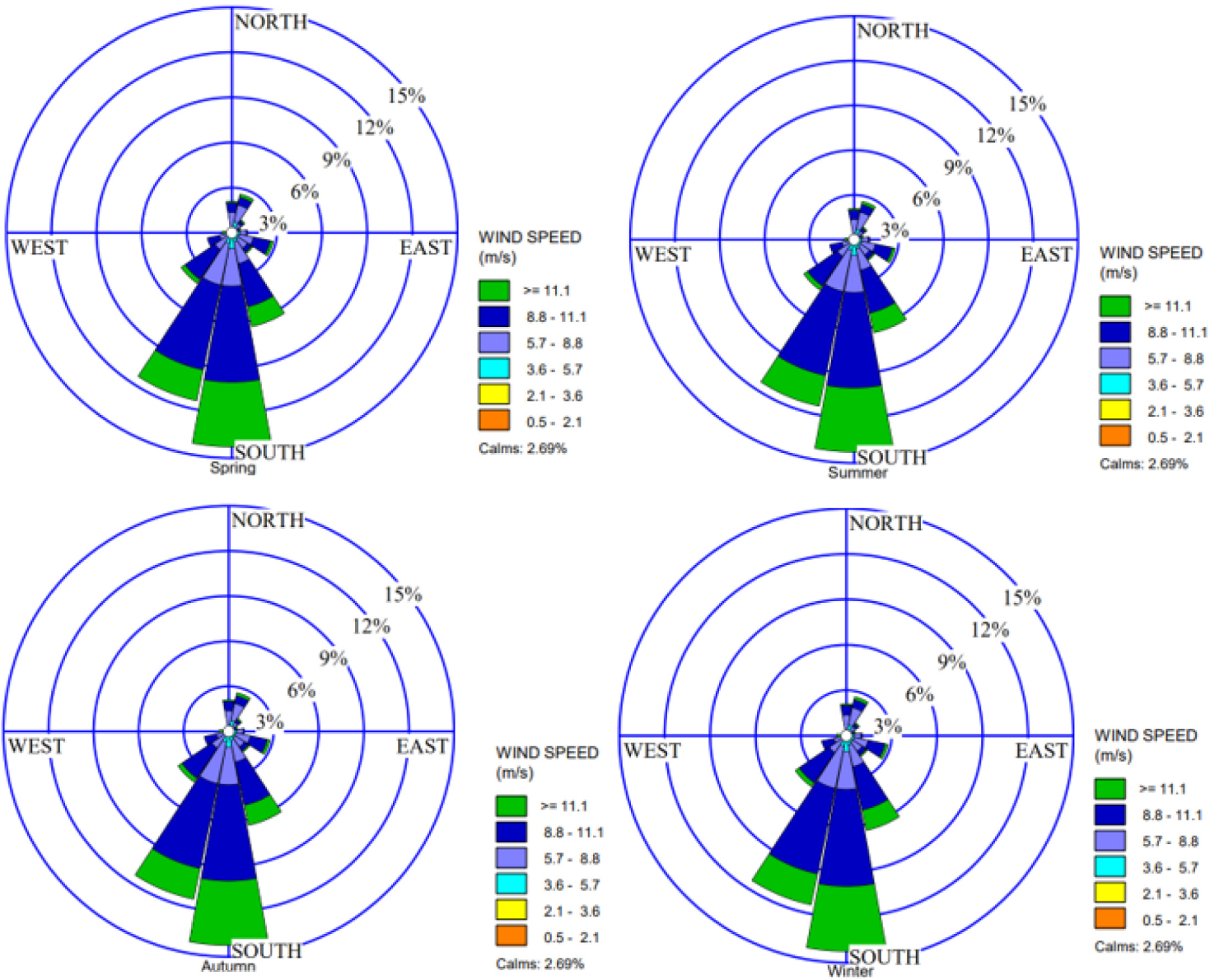
A wind rose serves as a graphical aid utilized by meteorologists to provide a concise depiction of the typical distribution of wind speed and direction at a specific location. The seasonal wind directions for 2021 and 2022 are illustrated by the wind rose depicted in Figure 3 and Figure 4 below. Typically, in wind data analysis, accurately predicting wind direction is paramount, particularly when strategizing the installation and micro siting of a wind turbine or wind farm. The seasonal wind rose was generated using WRPLOT version 7.0.0 software.
Seasonal windrose for 2021
Seasonal windrose for 2022
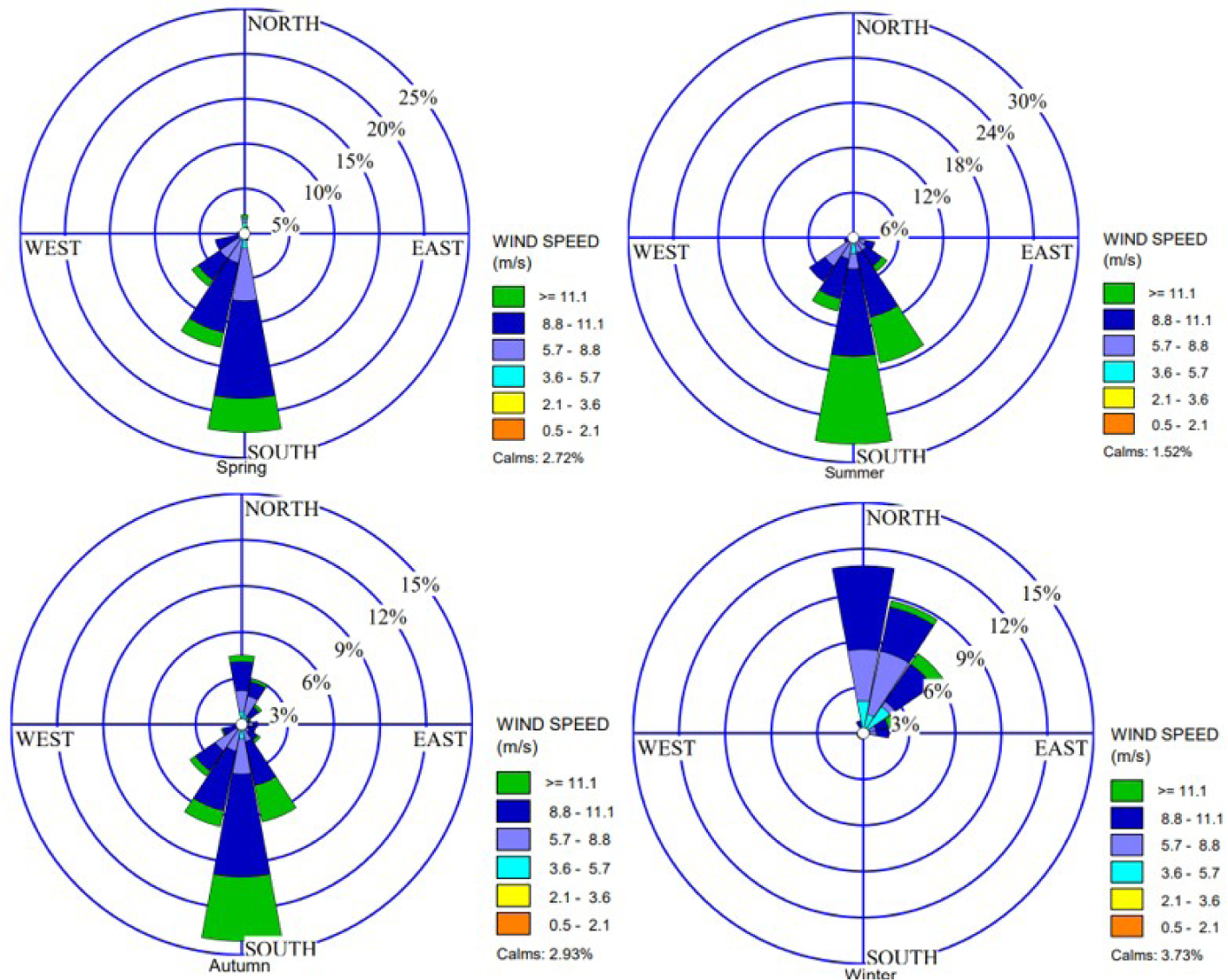
In 2021, it was observed that all seasons have the highest wind frequencies in the South (S) direction, comprising nearly 15% of occurrences, followed by South-Southwest (SSW) at 12%. Inversely, South-South East (SSE) and South-West (SW) had lower frequencies at 6.2% and 4% respectively. Other directions, such as North-East (NE) and South-East (SE), experienced frequencies below 3% across all seasons as illustrated in Figure 3. This indicates a predominant wind flow from the South during 2021. The calm number, representing minimal wind activity, was around 2.69% for each season.
In the spring, wind frequencies varied at 23% in the southern (S) direction, 13% in the South-West (SW) direction, and 8% in the South-South-West (SSW) direction. During the same season, there were no winds from the S, SW, or SSW in winter. Summer saw 18% of winds from the South-East (SE) and 8% in autumn. The Northern (N) direction experienced frequencies of about 7% in autumn and 14.5% in winter, while North-East (NE) winds were less frequent, with 3% in autumn and 12% in winter. Winter notably had a frequency of 6% in wind direction, in contrast to 0% in spring and summer. Wind flow from the East (E) was limited, comprising only 2% in autumn and less than 3% in winter.
In both 2021 and 2022, wind energy was most concentrated in the South (S) direction throughout all seasons except winter 2022, suggesting a consistent energy source. However, wind energy distribution varied seasonally, with shifts in frequencies among different directions. While the south remained dominant overall, other directions experienced notable changes in wind frequencies during specific seasons, indicating a seasonal shift in energy concentration influenced by prevailing wind patterns and strengths.
The annual Weibull parameters estimated from the four numerical methods are presented in Table 3, result shows that wind variability method had the largest Weibull parameters compare to other remaining methods. In both 2021 and 2022 the moment method exhibits the smallest value of shape factor of 1.578 and 1.602 respectively. Using all methods, the smallest shape factors were found in 2022 ranging between 11.2 to nearly 11.4 m/s.
Annual Weibull parameters using different methods
| Methods | 2021 | 2022 | ||
|---|---|---|---|---|
| k | c (m/s) | k | c (m/s) | |
| Standard Deviation | 1.592 | 12.430 | 1.616 | 11.228 |
| Energy Pattern | 1.799 | 12.538 | 2.675 | 11.314 |
| Moment Method | 1.578 | 12.420 | 1.602 | 11.220 |
| Variability | 2.771 | 12.526 | 2.632 | 11.320 |
In this research, four Weibull fitting methods were validated using three metrics, these are coefficient of determination (R2), Root Mean Square Error (RMSE), and Chi-square (χ2) test statistic. For both years, the Moment Method consistently achieved the best performance based on these criteria as Table 4 for 2021 and Table 5 for 2022. In 2021, Moment Method had the highest R2 of about 0.9998998 and lowest χ2 value of 27.116, the Standard Deviation Methods followed after Moment Method by having R2 of about 0. 0.9998995 and χ2 of 27.52091.
Validation metrics of the distribution fittings 2021
| Methods | RMSE | R2 | χ2 |
|---|---|---|---|
| Standard deviation | 0.106933 | 0.9998995 | 27.52091 |
| Energy Pattern | 0.106767 | 0.9998951 | 33.58586 |
| Moment Method | 0.106780 | 0.9998998 | 27.11629 |
| Wind Variability | 0.118400 | 0.9998768 | 61.89743 |
Validation metrics of the distribution fittings 2022
| Methods | RMSE | R2 | χ2 |
|---|---|---|---|
| Standard deviation | 0.002228 | 0.9999981 | 4.75968 |
| Energy Pattern | 0.002908 | 0.9999391 | 150.20152 |
| Moment Method | 0.002216 | 0.99995366 | 4.50878 |
| Wind Variability | 0.002875 | 0.99993988 | 127.04198 |
Moment Method also held the second lowest RMSE of about 0.106780 after Energy Pattern Factor with 0.106767. The moment method is considered to be the best method as according to these results in 2021. Similarly in 2022, Moment Method yielded the smallest RMSE and χ2 reaching 0.002216, and 4.50878 respectively, in case of R2, the Standard Deviation had the highest R2 (0.9999981). Based on these results, Moment Method was considered the most valid approach to characterize the wind speed distribution, with greater than 67% selection probability in both 2021 and 2022. Wind Variability Method was consistently attained the lowest R2 values. Therefore, quantitative validation using established metrics revealed Moment Method to provide the best fit/representation of the observed wind speeds over the investigation period. This robust technique is well-suited for analysing the wind energy potential at this site. Hence, all Weibull parameters taken after this validation were estimated using moment method as the best fit in this research.
The probability density function is used to show the proportion of time that a specific wind speed is likely to occur at a particular location. The density function for the study site is biased towards higher mean wind speed values, as shown in Figure 5a for both 2021 and 2022. The apex of the probability density function curve represents the wind speed that occurs most frequently. The analysis indicates that the wind speed at the site is expected to be highest in 2021 and 2022, with the most frequent wind speed being 7.9 m/s and 7.09 m/s, respectively. This suggests that the site experiences high wind speeds greater than 7 m/s for almost 70% of the time. Additionally, the data shows that in 2021, there was a greater spread of wind speeds towards higher values compared to 2022.
Annual probability (a) and cumulative probability (b) for 2021 and 2022
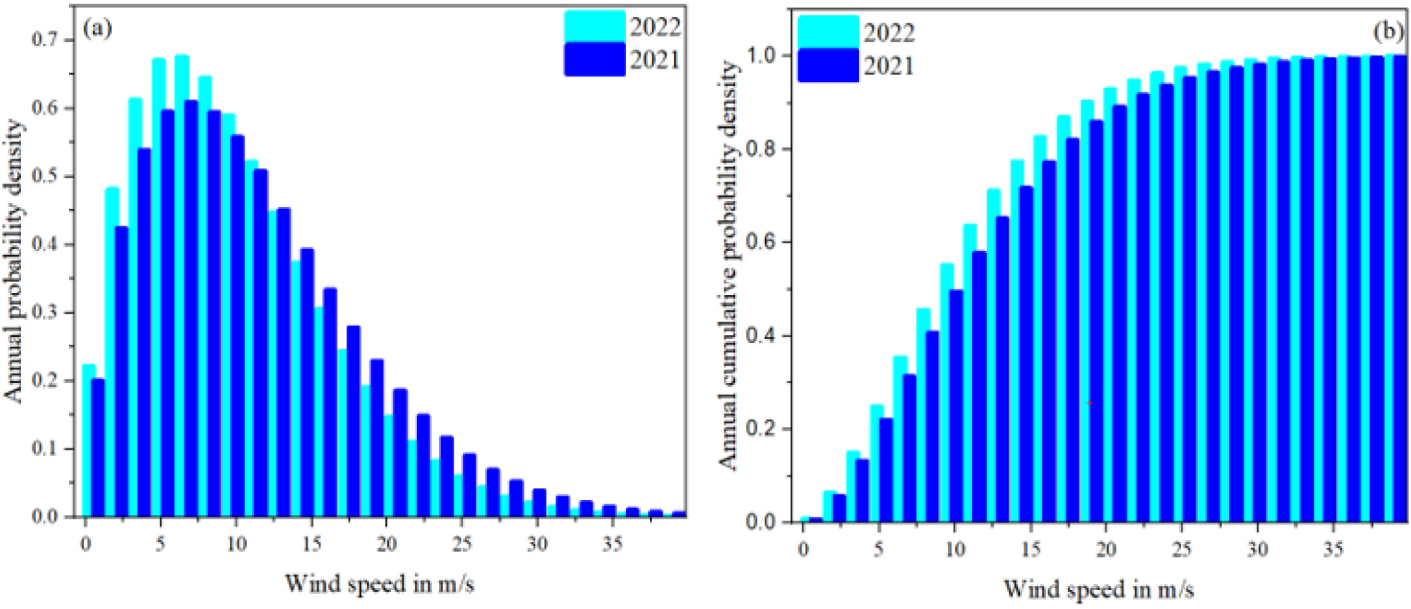
Figure 5b illustrates the cumulative probability distributions of wind speed at the study location for both 2021 and 2022. The cumulative distribution function can be used to estimate the duration of wind speeds within a specific range. This applies to wind speeds equal to or exceeding 2.5 m/s as an activation wind speed. The cumulative frequency values were higher in 2022 (99.94%) than in 2021 (99.78%), with a difference of approximately 0.16%.
Average wind speed is a commonly used metric in various applications, such as weather forecasting, environmental studies, and the design of structures like buildings and bridges. It provides a useful summary of the wind conditions at a specific site and can help assess the potential impacts of wind on various systems and activities. This research estimated monthly average wind speeds based on the best-fit Weibull parameters. The research findings indicate that the average annual wind speed in 2021 was 11.15 m/s, while in 2022 it was 10.06 m/s.
Table 6 shows that the monthly average and standard deviation wind speeds were higher in 2022 for small shape factors and large-scale factors compared to 2021. The data indicates that the highest monthly average wind speed occurred in October and November, with a value of 12.85 m/s, followed by December with 11.3 m/s. Conversely, the lowest average wind speed was recorded in January, February, and April, with a value of 5.966 m/s. It is noteworthy that wind speeds greater than 5.9 m/s were observed for more than eight months [33].
The average wind speed varied across the months in 2022. The highest average wind speeds were recorded in April (15.979 m/s), May (15.979 m/s), October (12.136 m/s), and November (12.136 m/s). In contrast, the lowest monthly averages were recorded in July and September, both at 8.303 m/s. The wind speed classification includes different classes: Calm wind (0-1.5 m/s), light breeze (1.6-3.3 m/s), gentle breeze (3.4-5.4 m/s), moderate breeze (5.5-7.9 m/s), fresh breeze (8.0-10.7 m/s), and strong breeze (10.8-13.8 m/s). Therefore, the wind speeds measured in this study fall under the strong breeze category. The study shows that, the site experiences constant wind resource since the average wind speed seems to be greater than the standard deviation.
Monthly Weibull parameters with their monthly average wind speed
| Months | 2021 | 2022 | ||||||
|---|---|---|---|---|---|---|---|---|
| k | c (m/s) | (m/s) | σ (m/s) | k | c (m/s) | (m/s) | σ(m/s) | |
| 1 | 1.66 | 6.68 | 5.97 | 4.10 | 1.55 | 11.79 | 10.60 | 7.00 |
| 2 | 1.66 | 6.68 | 5.97 | 4.00 | 1.54 | 7.19 | 9.84 | 6.60 |
| 3 | 1.72 | 8.41 | 7.50 | 5.70 | 2.61 | 12.80 | 11.37 | 5.00 |
| 4 | 1.66 | 6.68 | 5.97 | 4.20 | 2.20 | 18.04 | 15.98 | 7.70 |
| 5 | 1.94 | 8.40 | 7.45 | 4.70 | 1.46 | 17.65 | 15.98 | 11.20 |
| 6 | 1.95 | 10.14 | 9.00 | 5.30 | 1.47 | 10.02 | 9.07 | 0.30 |
| 7 | 1.94 | 9.27 | 8.22 | 5.10 | 1.50 | 9.20 | 8.30 | 6.00 |
| 8 | 1.95 | 10.14 | 9.00 | 5.60 | 1.55 | 10.70 | 9.63 | 6.40 |
| 9 | 1.95 | 11.88 | 10.54 | 6.50 | 1.50 | 9.20 | 8.30 | 6.00 |
| 10 | 1.96 | 14.49 | 12.85 | 7.80 | 1.00 | 12.15 | 12.14 | 12.00 |
| 11 | 1.96 | 14.49 | 12.85 | 7.80 | 1.58 | 13.52 | 12.14 | 7.90 |
| 12 | 1.95 | 12.67 | 11.31 | 6.90 | 1.55 | 11.79 | 10.60 | 7.00 |
In many feasibility studies for wind power projects, assessing the twelve-monthly airstream power and energy generation is very important for determining the viability and potential profitability of the projects. The yearly breeze power and energy are important in many aspects such as in Energy Production Estimation, Cost-Benefit Analysis, and Resource Assessment. The annual power estimated in this study shows that during 2021, the total wind power potential was about 2145.74 W/m2 while in 2022, the total wind power density was 1543.05 W/m2. This shows that, in 2022 an expected annual power was smaller compare to that of 2021, hence this had direct effect and made a difference to an annual energy density between 2021 and 2022.
In 2021, the monthly wind power density fluctuated between 351.7 and 2957.7 W/m², while in 2022, it varied between 434.7 and 7048.5 W/m². For the spring months (March, April, and May), wind power ranged from 374.1 to 855.9 W/m² in 2021 and 1375.6 to 7048.5 W/m² in 2022. During the summer months (June, July, and August), wind power ranged from 803.7 to 1043 W/m² in 2021 and 950 to 1423.4 W/m² in 2022. For autumn (September, October, and November) and winter (December, January, and February), wind power density ranged from 1653.9 to 2957.7 and 351.7 to 2033.3 W/m² in 2021, respectively, and from 950 to 2767.21 and 434.7 to 1889.7 W/m² in 2022.
Table 7 presents monthly wind power and energy density data for t 2021 and 2022. Wind energy potential is closely linked to wind power density, as the latter is a critical factor determining the feasibility and efficiency of wind energy generation in a specific location. Wind power density measures the available wind energy at a given location and is influenced by factors such as wind speed and air density. Understanding this connection is essential for evaluating the viability of wind energy projects and optimizing their performance. The corresponding monthly wind energy variation is highly dependent on the significant variation of the wind power density of the respective month, season, or year. This means that the time of the high wind power generation is considered to have the high energy density, the year 2021 included September, October, November, and December with individual wind energy densities of 1190.778, 2200.552, 2129.567, and 1512.749 MWh/m2 respectively, while the other months have a wind energy density ranging between 236.355 and 776.01 MWh/m2.
Monthly wind power and energy density
| Months | 2021 | 2022 | ||
|---|---|---|---|---|
| P/A (W/m2) | E/A (MWh/m2) | P/A (W/m2) | E/A (MWh/m2) | |
| 1 | 351.739 | 261.694 | 1,889.736 | 1,405.964 |
| 2 | 351.719 | 236.355 | 434.703 | 292.120 |
| 3 | 855.919 | 636.804 | 1,375.645 | 1,023.480 |
| 4 | 374.097 | 269.349 | 4,361.021 | 3,139.935 |
| 5 | 604.502 | 449.749 | 7,048.452 | 5,244.049 |
| 6 | 982.784 | 707.604 | 1,275.444 | 918.320 |
| 7 | 803.795 | 598.023 | 950.014 | 706.810 |
| 8 | 1,043.018 | 776.005 | 1,423.350 | 1,058.972 |
| 9 | 1,653.859 | 1,190.778 | 950.014 | 684.010 |
| 10 | 2,957.732 | 2,200.552 | 6,511.441 | 4,844.512 |
| 11 | 2,957.732 | 2,129.567 | 2,767.312 | 1,992.465 |
| 12 | 2,033.264 | 1,512.749 | 1,889.736 | 1,405.964 |
For the year 2022, more than 80% of all months were found to have a minimum wind energy density of about 1023.480 MWh/m2 and a maximum wind energy density of about 5244.049 MWh/m2 while only four months were found to have wind energy density ranging between 292 to 919 MWh/m2. Due to this result, there is a strong logical argument to conclude that wind energy potential sustainability was higher during 2022 in comparison to the year 2021.In general, the large wind power and energy density of the site can be attributed to many factors such as temperature gradients leading to stronger pressure differences, which in turn drive stronger winds, low pressure systems which generate stronger winds as air flows from areas of high pressure to areas of low pressure, frontal boundaries, polar jet streams, and less stable atmosphere.
• Wind Power Classification and sustainability status
In consideration to NREL wind power classification for the wind resource assessment, the site seems to have good wind energy potential sustainability as shown in Table 8 For the annual wind power, the site had class 7 in both 2021 and 2022, this means that the is highly desirable for large-scale wind energy projects. For the monthly assessment, the study shows that, during the year 2021, more than 8 months of the year have class 7 while out of the remaining four months, three months (January, February, and April) were categorized in class 3 this means that the wind resources have moderate average wind speeds, making them potentially suitable for small-scale wind energy projects.
Wind power classification according to National Renewable Energy Laboratory [34]
| Category | Power interval (W/m2) | Potential status |
|---|---|---|
| 1 | 0 to 0.2 | Unsuitable |
| 2 | 0.2 to 0.3 | Appropriate for Independent Use |
| 3 | 0.3 to 0.4 | Decent |
| 4 | 0.4 to 0.5 | Decent |
| 5 | 0.5 to 0.6 | Excellent |
| 6 | 0.6 to 0.8 | Outstanding |
| 7 | 0.8 to 2.0 | Superb |
The month of May was categorized into Class 5, which means that, during that time the areas have excellent wind energy potential and are often chosen for large wind farms. Also, during the year 2022, more than eleven months were classified in class 7 which is characterized by superior wind speeds, which can lead to exceptional energy production. Class 7 areas are rare and highly desirable for large-scale wind energy projects. The remaining month (February) was classified as Class 4, which means that Class 4 wind resources have reasonably good wind speeds, making them suitable for utility-scale wind energy projects. The study area had an economically viable opportunity for airstream energy development.
The average power of a wind turbine represents the typical electrical power it produces over a specific time period and is usually quantified in watts (W) or kilowatts (kW). This research involved the calculation and examination of the annual average power outputs of the chosen wind turbines. As per as in eq. (26), the seven-wind turbine were assessed in this research and their specifications are indicated in Table 9 below
Specification of proposed turbines [18]
| Parameters | `P15-50 | P19-100 | WES30 | P50-500 | P62-1000 | WWD-1-60 | B-1000-54 |
|---|---|---|---|---|---|---|---|
| PeR (Kw) | 50 | 10 | 250 | 500 | 1000 | 1000 | 1000 |
| h(m) | 30 | 30 | 36 | 50 | 60 | 70 | 45 |
| d (m) | 15.2 | 19.1 | 30 | 50 | 62 | 60 | 54 |
| vc (m/s) | 2.5 | 2.5 | 2.7 | 2.5 | 2.5 | 3.6 | 3 |
| vr (m/s) | 10 | 12 | 12.5 | 12 | 12 | 12.5 | 14 |
| vf (m/s) | 25 | 25 | 25 | 25 | 25 | 25 | 25 |
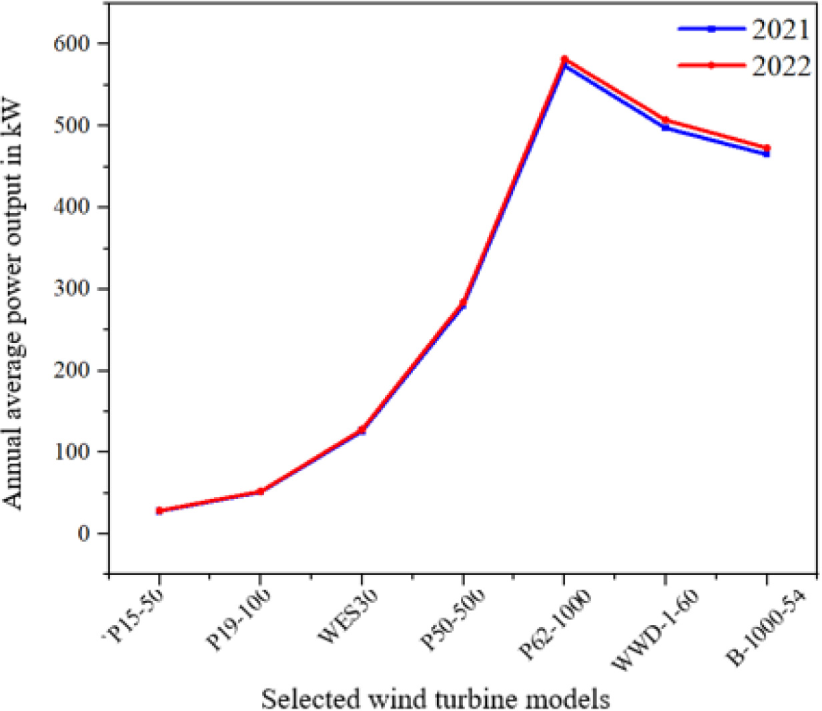
In both 2021 and 2022, the wind turbine that exhibited the highest power output was the POLARIS P62-1000, with 573.84 kW in 2021 and 582.06 kW in 2022 as shown in Figure 6. Following closely were the WWD-1-60 and BONUS B-1000-54 turbines. For the WWD-1-60 turbine, the average power generated in 2021 and 2022 was 497.43 kW and 507.36 kW, respectively. Meanwhile, for the BONUS B-1000-54 turbine, the average power generated in 2021 and 2022 stood at 465.28 kW and 473.05 kW, respectively. On the other hand, turbine models with the lowest average power included POLARIS P15-50, producing 28.08 kW in 2021 and 28.55 kW in 2022, followed by the POLARIS P19-100, with respective average powers of 51.44 kW and 42.24 kW for 2021 and 2022 respectively. There were no significant differences in annual power output between all turbines when compared the power delivered in 2021 and 2022.
Annual power output of the proposed turbines
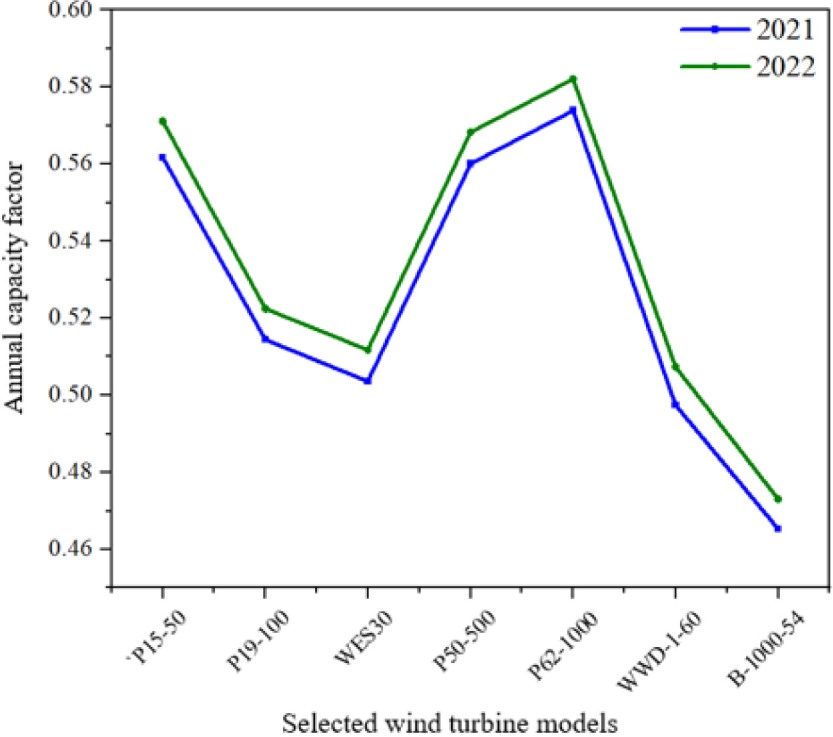
In consideration of the annual capacity factor for both 2021 and 2022, the maximum capacity factor was obtained in the POLARIS P62-1000 model counting 0.57334 (57.38%) for the year 2021 and 0.5820 (58.20%) in 2022 followed by both POLARIS P15-50 and POLARIS P50-500. The annual capacity factor variation for 2021 and 2022 is shown in the Figure 7 below. The model POLARIS P15-50 has an annual capacity factor of 0.5656 (56.56%) and 0.5144 (51.44%), the model POLARIS P50-500 has an annual capacity factor of 57.38% for the year 2021 and 56.83% for the year 2022. The turbine models POLARIS P19-100, WES30, and WWD-1-60 have capacity factors ranging between 49 to 52.24% for both years 2021 and 2022 respectively.
Annual capacity factor of the proposed wind turbines
The monthly average power for the years 2021 and 2022 is shown in the Table 10 and Table 11 respectively. The results of the monthly performance analysis of the selected wind turbine models show that, during both the years 2021 and 2022, the model with the smallest monthly power between January and December was POLARIS P15-50 followed by P19-100 and WES30. The average power output generated by the POLARIS P15-50 ranged between 21 and 28 kW and between 23 and 36 kW for the years 2021 and 2022 respectively. Also, during the year 2021, the POLARIS P19-100 and WES30 have monthly average power ranging between 37 to 51 kW and 91 to 124 kW respectively while in 2022 the average power generated by POLARIS P19-100 and WES30 ranged between 35 to 66 kW and 102 to 151 kW respectively.
Monthly wind turbine power output in kW for 2021
| Months | P15-50 | P19-100 | WES30 | P50-500 | P62-1000 | WWD-1-60 | B-1000-54 |
|---|---|---|---|---|---|---|---|
| 1 | 23.934 | 39.387 | 96.452 | 220.813 | 460.911 | 433.467 | 345.747 |
| 2 | 22.520 | 39.780 | 97.235 | 211.560 | 431.728 | 396.189 | 358.483 |
| 3 | 22.820 | 41.211 | 100.109 | 211.616 | 426.617 | 390.721 | 369.042 |
| 4 | 21.436 | 37.870 | 91.917 | 198.608 | 403.853 | 365.858 | 335.773 |
| 5 | 25.379 | 45.168 | 109.829 | 233.986 | 473.404 | 437.156 | 402.897 |
| 6 | 28.156 | 50.875 | 123.835 | 258.366 | 517.654 | 484.233 | 457.113 |
| 7 | 27.240 | 49.012 | 119.538 | 251.623 | 506.040 | 472.288 | 441.817 |
| 8 | 27.746 | 50.147 | 122.016 | 254.721 | 510.598 | 476.945 | 450.287 |
| 9 | 27.952 | 51.055 | 123.660 | 253.006 | 502.210 | 469.077 | 455.283 |
| 10 | 27.456 | 50.552 | 122.019 | 246.415 | 486.681 | 455.399 | 448.585 |
| 11 | 27.367 | 50.361 | 121.658 | 246.408 | 487.553 | 456.394 | 447.685 |
| 12 | 27.746 | 50.794 | 122.938 | 251.086 | 498.478 | 465.999 | 452.659 |
Monthly wind turbine power output in kW for 2022
| Months | `P15-50 | P19-100 | WES30 | P50-500 | P62-1000 | WWD-1-60 | B-1000-54 |
|---|---|---|---|---|---|---|---|
| 1 | 33.888 | 61.267 | 150.665 | 316.859 | 638.677 | 615.642 | 562.179 |
| 2 | 23.747 | 42.133 | 102.939 | 222.217 | 452.006 | 416.745 | 379.779 |
| 3 | 36.001 | 65.501 | 159.541 | 326.564 | 648.555 | 619.922 | 588.739 |
| 4 | 29.355 | 54.603 | 131.629 | 261.490 | 513.273 | 486.307 | 484.334 |
| 5 | 23.188 | 42.942 | 103.609 | 209.567 | 414.788 | 385.864 | 381.902 |
| 6 | 25.100 | 45.654 | 110.791 | 230.398 | 461.016 | 426.568 | 408.706 |
| 7 | 25.609 | 46.318 | 112.705 | 236.306 | 474.447 | 439.914 | 416.296 |
| 8 | 26.488 | 48.193 | 116.936 | 242.197 | 483.802 | 449.894 | 431.196 |
| 9 | 25.571 | 46.253 | 112.541 | 235.943 | 473.703 | 439.157 | 415.685 |
| 10 | 19.049 | 35.146 | 84.831 | 174.820 | 348.518 | 316.933 | 312.735 |
| 11 | 26.286 | 48.277 | 116.714 | 237.932 | 472.200 | 440.140 | 429.797 |
| 12 | 26.259 | 47.991 | 116.226 | 238.988 | 475.962 | 442.615 | 428.243 |
Also, the turbine models with the medium monthly average power during all months of the year 2021 and 2022 were P50-500, WWD-1-60, and BONUS B-1000-54. During the year 2021, P50-500 generated the monthly average power ranging between 198 to 259 kW while the respective monthly average power generated by the WWD-1-60 and BONUS B-1000-54 was ranging between 316 to 620 kW and 335 to 458 kW. On the other hand, during the year 2022, POLARIS P19-500 generated the monthly average power ranging between 174 to 327 kW while WWD-1-60 and B-1000-54 have the average power ranging between 316 to 616 kW and 312 TO 589 kW respectively.
The results also show that POLARIS P62-1000 has the largest monthly average power output among all selected wind turbines. In 2021, P62-1000 generated the monthly average power ranging between 403 to 518 kW while in the year 2022, this turbine model generated the monthly average power ranging between 348 to 649 kW. This result indicates that, among all selected wind turbine models, the POLARIS P62-1000 has a high tendency to generate large power at the site.
The monthly wind turbine capacity factor can vary significantly depending on the location of the wind farm, the specific design of the wind turbines, and the prevailing weather conditions. Wind energy developers and operators typically monitor and analyze these variations to optimize the performance and revenue generation of their wind farms. Table 12 show the monthly capacity factors of this research for the year 2021 while the capacity factor variation for the year 2022 is shown in the Table 13 below.
The results show that, during the year 2021 and 2022, the largest monthly Cf were obtained from POLARIS 15-50 with the interval range between 42 to 57% and 38 to 68% respectively, although this model has the smallest monthly average power compare to other models. The capacity factor of POLARIS P19-100, WES30 and POLARIS P50-500 have the monthly Cf intervals ranging from 37 to 52%, 36 to 50%, and from 39 to 52% respectively. The wind turbine model WWD-1-60 and BONUS B-1000-54 have the monthly Cf ranging from 36 to 49% and 33 to 46% respectively. The POLARIS P62-1000 was found to have the second largest monthly capacity factors ranging between 40 and 52% although it has the largest monthly average power compare to all selected wind turbine models.
Monthly performance of wind turbine power for 2021
| Months | `P15-50 | P19-100 | WES30 | P50-500 | P62-1000 | WWD-1-60 | B-1000-54 |
|---|---|---|---|---|---|---|---|
| 1 | 0.4787 | 0.3939 | 0.3858 | 0.4416 | 0.4609 | 0.4335 | 0.3457 |
| 2 | 0.4504 | 0.3978 | 0.3889 | 0.4231 | 0.4317 | 0.3962 | 0.3585 |
| 3 | 0.4564 | 0.4121 | 0.4004 | 0.4232 | 0.4266 | 0.3907 | 0.3690 |
| 4 | 0.4287 | 0.3787 | 0.3677 | 0.3972 | 0.4039 | 0.3659 | 0.3358 |
| 5 | 0.5076 | 0.4517 | 0.4393 | 0.4680 | 0.4734 | 0.4372 | 0.4029 |
| 6 | 0.5631 | 0.5087 | 0.4953 | 0.5167 | 0.5177 | 0.4842 | 0.4571 |
| 7 | 0.5448 | 0.4901 | 0.4782 | 0.5032 | 0.5060 | 0.4723 | 0.4418 |
| 8 | 0.5549 | 0.5015 | 0.4881 | 0.5094 | 0.5106 | 0.4769 | 0.4503 |
| 9 | 0.5590 | 0.5105 | 0.4946 | 0.5060 | 0.5022 | 0.4691 | 0.4553 |
| 10 | 0.5491 | 0.5055 | 0.4881 | 0.4928 | 0.4867 | 0.4554 | 0.4486 |
| 11 | 0.5473 | 0.5036 | 0.4866 | 0.4928 | 0.4876 | 0.4564 | 0.4477 |
| 12 | 0.5549 | 0.5079 | 0.4918 | 0.5022 | 0.4985 | 0.4660 | 0.4527 |
Monthly performance of wind turbine power for 2022
| Months | P15-50 | P19-100 | WES30 | P50-500 | P62-1000 | WWD-1-60 | B-1000-54 |
|---|---|---|---|---|---|---|---|
| 1 | 0.6778 | 0.6127 | 0.6027 | 0.6337 | 0.6387 | 0.6156 | 0.5622 |
| 2 | 0.4749 | 0.4213 | 0.4118 | 0.4444 | 0.4520 | 0.4167 | 0.3798 |
| 3 | 0.7200 | 0.6550 | 0.6382 | 0.6531 | 0.6486 | 0.6199 | 0.5887 |
| 4 | 0.5871 | 0.5460 | 0.5265 | 0.5230 | 0.5133 | 0.4863 | 0.4843 |
| 5 | 0.4638 | 0.4294 | 0.4144 | 0.4191 | 0.4148 | 0.3859 | 0.3819 |
| 6 | 0.5020 | 0.4565 | 0.4432 | 0.4608 | 0.4610 | 0.4266 | 0.4087 |
| 7 | 0.5122 | 0.4632 | 0.4508 | 0.4726 | 0.4744 | 0.4399 | 0.4163 |
| 8 | 0.5298 | 0.4819 | 0.4677 | 0.4844 | 0.4838 | 0.4499 | 0.4312 |
| 9 | 0.5114 | 0.4625 | 0.4502 | 0.4719 | 0.4737 | 0.4392 | 0.4157 |
| 10 | 0.3810 | 0.3515 | 0.3393 | 0.3496 | 0.3485 | 0.3169 | 0.3127 |
| 11 | 0.5257 | 0.4828 | 0.4669 | 0.4759 | 0.4722 | 0.4401 | 0.4298 |
| 12 | 0.5252 | 0.4799 | 0.4649 | 0.4780 | 0.4760 | 0.4426 | 0.4282 |
In other hand, for the year 2022, the wind turbine models POLARIS P19-100, WES20, POLARIS P50-500, WWD-1-60 and BONUS B-1000-54 have the monthly capacity factors ranging between 35 and 52% while the POLARIS P62-1000 has the second largest monthly Cf between 46 and 64%, also it has the largest monthly average power throughout the months of the year. In December, the capacity factor ranged between 40 and 57%, while the remaining months have the capacity factors ranging between 34 to 48%. In contrast, during the year 2022, the months with largest monthly capacity factors includes March, April, June, August, September, November, December and January, these months have the capacity factors ranging between 31 to 73%. The remaining months of February, May and October; have the Cf was ranging between 38 and 48%. For this result, it means that all turbines are cost effective for all months.
The effectiveness of all seven wind turbines (WTs) has been confirmed, with the P62-1000, WWD-1-60, B-1000-54, and P50-500 emerging as the most efficient. These top performers owe their effectiveness to their height and rotor diameter. Indeed, the height and rotor diameter of a WT significantly influence its ability to convert wind power (WP) into electrical power. Taller turbines benefit from higher wind speeds (WSs), reduced turbulence, and access to more consistent wind resources at greater heights. However, taller towers come with increased construction costs. The heights of the leading WTs 62-1000, WWD-1-60, and B-1000-54 were 60, 70, 45, and 50 meters respectively, while the others ranged between 30 and 36 meters. Additionally, turbines with larger rotor diameters can capture more wind power, enhancing power output and efficiency, particularly at lower wind speeds. This was evident in the research, where the top four WTs had blade diameters ranging from 50 to 62 meters. Despite the higher initial investment for taller towers and larger rotor diameters, the boosted energy production often justifies these costs, especially in areas with lower wind speeds. Thus, the P62-1000 was chosen as the most high-performance WT for the site. Nevertheless, since all WTs analysed in the study proved cost-effective annually, seasonally, and monthly, any of them could be selected based on the investment budget or cost-benefit analysis of the investment plan.
Numerical analysis of potential wind on Zanzibar Coastal Island was done. The moment method has the best fit compare to other numerical method applied in this research. Both annual, seasonal, and monthly have more than 60% average wind speeds classified in fresh breeze zone with wind speed range between 5.5 and 7.9 m/s and more than 20% in a strong breeze zone with the wind speed range between 8 and 10.7 m/s while the remaining are in gentle breeze zone with the wind speed range between 3.4 to 5.4 m/s.
Also, the site found to have sustainable wind energy potential, more than 85% of all months of the year 2021 and 2022 have the wind energy potential ranging between class 4 to class 7 while the remaining are in class 2 and 3 based on the NREL wind power classification.
The wind turbine model POLARIS P62-1000 was found to have the largest annual, seasonal and monthly average powers compare to all wind turbine models analyzed in this research. This means that, based on the power generation, the POLARIS P62-1000 is recommended as the best wind turbine model to be installed at the site.
The calculated annual, Seasonal and monthly capacity factors of all wind turbine models were found to range between 40 to 71% which are greater than 25%. In consideration of the capacity factor, P15-50 has the largest capacity factor but the smallest power output. POLARIS P62-1000 has the second largest capacity factor with no significant difference compare to P15-50, hence the model P62-1000 is the most favorable wind turbine model to be installed at the site based on both performance and power output, yet other factors like economic status of the investor may be considered since all turbines are cost effective as they have capacity factors greater than 25%.
The authors are highly acknowledging the Ministry of Education, Culture, Research and Technology of Indonesia through the Faculty of Engineering, Universitas Sebelas Maret for all supports including financial acquisition under scheme of “Penelitian kolaborasi Internasional (KI-UNS)” with financial aid of HIBAH non APBN, and contract number 194.2/UNS27.22/PT.01.03/2024.
| Cf | capacity factor of the turbine | [-] |
| E | wind energy density | [kWh/m2] |
| H | tower height | [m] |
| P | wind power density | [W/m2] |
| Pe | average power of the wind turbine | [kW] |
| Pr | nominal power of the wind turbine | [kW] |
| v | mean wind speed | [m/s] |
| vc | starting speed of the wind turbine | [m/s] |
| vf | ceasing speed of the wind turbine | [m/s] |
| vm | maximum wind speed | [m/s] |
| vp | likely wind speed | [m/s] |
| vr | nominal speed of the wind turbine | [m/s] |
| ρ | density | [kg/m3] |
| σ | speed standard deviation | [m/s] |
| Γ | gamma function | [-] |
- Renewable energy and biodiversity: Implications for transitioning to a Green Economy, 2017,
- T.S.N. Linear Modelling of Water Potential and Supply for Decentralized Energy-, 2022,
- Evaluation of different turbine concepts for wind power, 2008,
- Analysing the Role of Renewables in Energy Security by Deploying Renewable Energy Security Index, 2023,
- Wind Speed Distributions Used in Wind Energy Assessment: A Review, 2021,
- Wind energy potential assessment based on wind speed, its direction and power data, 2021,
- Statistical properties of electricity generation from a large system of wind plants and demand for fast regulation, 2017,
- Assessment of Power Coefficient of an Offline Wind Turbine Generator System, 2013,
- Performance evaluation of wind decontamination system by computational fluid dynamics, 2014,
- A new method to estimate Weibull parameters for wind energy applications, 2009,
- An investigation of wind power density distribution at location with low and high wind speeds using statistical model, 2018,
- Method to Model the Hourly Variability of Renewable Energy Sources in Integrated Assessment Models, 2024,
- Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application, 2011,
- Assessment of Wind Energy Potentiality at Ajloun, Jordan Using Weibull Distribution Function, 2022,
- Comparative Study of Five Methods to Estimate Weibull Parameters for Wind Speed on Phangan Island, Thailand, 2015,
- Assessment of wind energy for small-scale wind power in Chuuk State, Micronesia, 2015,
- Wind Power in Indonesia: Potential, Challenges, and Current Technology Overview, 2022,
- Estimating the potential of wind energy resources using Weibull parameters: A case study of the coastline region of Dar es Salaam, 2021,
- Analysis of wind speed data and wind energy potential in Faya-Largeau, Chad, using Weibull distribution, 2018,
- Wind energy potential assessment in Naxos Island, Greece, 2010,
- A review of wind speed probability distributions used in wind energy analysis. Case studies in the Canary Islands, 2009,
- An Assessment of Wind Energy Potential for the Three Topographic Regions of Eritrea, 2020,
- Estimation of the wind energy potential for coastal locations in India using the Weibull model, 2020,
- Evaluation of wind energy potential and trends in Morocco, 2019,
- An assessment of wind energy potential as a power generation source in the capital of Iran, Tehran, 2010,
- Analysis of wind speed data and wind energy potential in three selected locations in south-east Nigeria, 2012,
- Performance analysis of numerical methods for determining Weibull distribution parameters applied to wind speed in Mato Grosso do Sul, Brazil, 2022,
- Wind speed and power density analysis based on Weibull and Rayleigh distributions (A case study: Firouzkooh county of Iran) $, 2015,
- Evaluation of the Technical Wind Energy Potential of Kisii Region Based on the Weibull and Rayleigh Distribution Models, 2021,
- The Weibull distribution function and wind power statistics, https://www.researchgate.net/publication/234452780
- Wind speed data and wind energy potential using Weibull distribution in Zagora, Morocco, 2019,
- Performance analysis of numerical methods for determining Weibull distribution parameters applied to wind speed in Mato Grosso do Sul, Brazil, 2022,
- Data-driven energy consumption prediction leveraging historical data and environmental factors in buildings, 2024,
- Exploring wind energy potential as a driver of sustainable development in the southern coasts of iran: The importance of wind speed statistical distribution model, 2021,




